Fantastic Tips About How To Do Large Division

Tackling the Beast

1. Understanding the Challenge

Let's be honest, seeing a large division problem can make anyone's palms sweat a little. All those digits staring back at you, whispering promises of potential errors and frustrating calculations. But don't fret! Large division, while seemingly intimidating, is simply a series of smaller, manageable steps. Think of it like eating an elephant — one bite at a time! We're going to break down the process, so you can confidently tackle even the most monstrous division problems.

Many of us have been there, struggling to remember the exact steps, getting lost in the process and ending up with a number that seems completely out of sync. The key is to really understand the why behind each step, not just how to do it. Once you grasp the logic, the steps become much more intuitive, and you'll find yourself navigating those large numbers with surprising ease. We'll cover long division, the tried-and-true method that forms the foundation for more advanced techniques.

Imagine you're sharing a giant pizza with a group of friends. You need to figure out how many slices each person gets if you want to make sure everyone gets an equal share. That's essentially what division is all about: splitting something into equal parts. This skill isn't just for math class; it's useful in everyday life, from splitting bills to figuring out how many hours to work on a project each day.

So, take a deep breath, grab a pencil and paper (or your favorite digital note-taking tool), and let's embark on this journey together. We'll demystify the process and transform you from a division-dreader to a division-doer. No more number anxiety! Are you ready? I know you are!

The Long Division Breakdown

2. Setting Up the Problem

Okay, let's get our hands dirty! The first step in any long division problem is to set it up correctly. Think of it like staging a play — get the actors (numbers) in the right positions before the action begins. You'll have your dividend (the number being divided), your divisor (the number you're dividing by), and a cozy little spot above the dividend where the quotient (the answer) will eventually reside.

The dividend goes inside the division bracket (also sometimes referred to as the division "house"), and the divisor sits outside to the left. Make sure you have enough space above the dividend to write your quotient, one digit at a time. This is where neatness counts, believe me. It will save you from making errors in the process. No one wants to get all the way to the end just to realize they misplaced a number.

For example, if you're dividing 756 by 21, 756 goes inside the division bracket, and 21 sits comfortably to its left. Now, give yourself a little pat on the back; you've already conquered a crucial first step! You're on your way to large division mastery! Really though, the visual setup is important, so practice this a little.

Before we jump into the actual dividing, let's just double-check that we understand what we are about to do. We want to know how many times the number outside the bracket (the divisor) fits into the number inside the bracket (the dividend). It's like trying to figure out how many 21-seater vans you need to transport 756 people.

The Long Division Breakdown

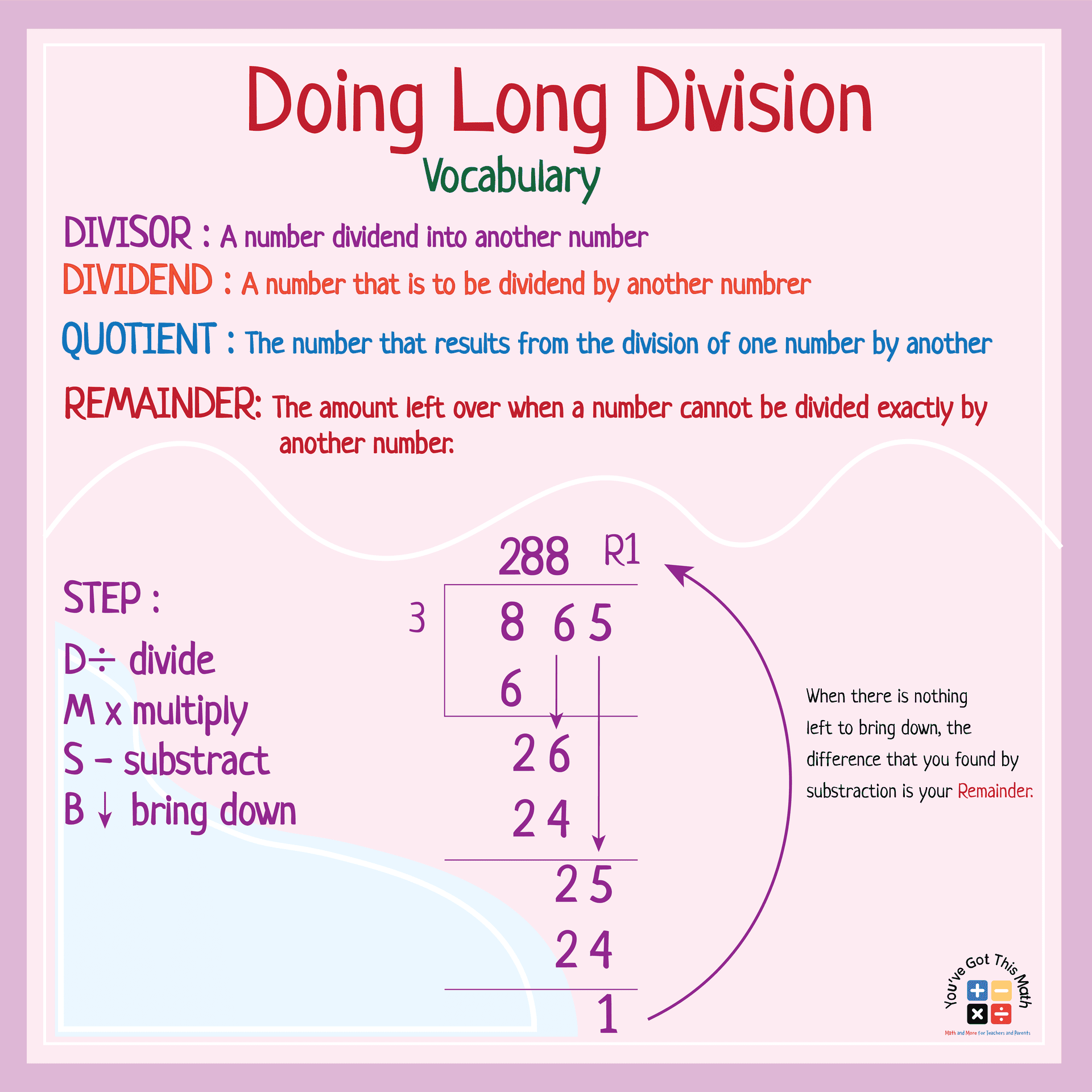
3. Divide, Multiply, Subtract, Bring Down & Repeat

Now comes the real action! Here's where you implement the core long division rhythm: Divide, Multiply, Subtract, Bring Down. Think of it as a dance — once you learn the steps, you can glide through any division problem with grace and efficiency. Let's break it down with an example, sticking with our 756 21 problem.

First, Divide: How many times does 21 go into 7? Well, it doesn't (zero times). So, we look at the next digit, making it 75. How many times does 21 go into 75? It goes in 3 times. Write the '3' above the '5' in the dividend (that's the start of your quotient!). Next, Multiply: Multiply the divisor (21) by the quotient digit we just wrote (3). 21 x 3 = 63. Write the '63' under the '75'.

Now, Subtract: Subtract 63 from 75. 75 - 63 = 12. Write '12' below the '63'. Then, Bring Down: Bring down the next digit from the dividend (the '6') and write it next to the '12', forming '126'. Repeat these steps with the new number (126). How many times does 21 go into 126? It goes in 6 times. Write '6' next to the '3' in the quotient (above the division bracket).

Multiply 21 by 6, which equals 126. Write this under the 126 you already had. Subtract 126 from 126, and you get 0. Since there are no more digits to bring down, and the remainder is 0, you're done! The answer (the quotient) is 36. So, 756 21 = 36. See? Not so scary after all! Practice makes perfect, so keep repeating the Divide, Multiply, Subtract, Bring Down steps until you feel like a division ninja.

Dealing with Remainders

4. What Happens When It Doesn't Divide Evenly?

Sometimes, life isn't neat and tidy, and neither are division problems. You might find yourself in a situation where the divisor doesn't divide evenly into the dividend, leaving you with a remainder. Don't panic! Remainders are perfectly normal, and there are a few ways to deal with them.

The simplest way is to just leave it as a remainder. For example, if you divide 17 by 5, you get 3 with a remainder of 2 (written as 3 R2). This means 5 goes into 17 three times, with 2 left over. You can also express the remainder as a fraction. In the same example, 3 R2 can be written as 3 2/5. This means 5 goes into 17 three and two-fifths times.

Another option, particularly useful in decimal calculations, is to add a decimal point and a zero to the dividend, and continue the division. For instance, if you were dividing 17 by 5 and wanted a decimal answer, you'd add ".0" to 17, making it 17.0. Then, bring down the '0' and continue dividing. In this case, 5 goes into 20 four times, so the answer would be 3.4. The appropriateness of each method depends on the context of the problem. A pizza can't have a partial slice in reality!

Knowing how to handle remainders is essential for real-world applications of division. Whether it's splitting a restaurant bill, measuring ingredients for a recipe, or calculating fabric lengths, remainders often play a crucial role. Mastering this concept will expand your division skillset, helping you confidently approach a wider variety of division problems. Now, I challenge you to find one that doesn't result in a whole number!

Tips and Tricks for Large Division Success

5. Making Life Easier

Let's be honest, no one loves doing long division, especially with large numbers. But there are some clever strategies you can employ to make the process smoother and less prone to errors. First, practice your multiplication tables. Knowing your facts inside and out will speed up your calculations considerably. A good knowledge of multiplication will make short work of solving large division problems!

Next, estimate before you start. Round the dividend and divisor to the nearest convenient number to get a rough idea of the quotient. This will help you catch any major errors along the way. For instance, if you're dividing 1452 by 23, you could round to 1400 20, which is approximately 70. So, you know your answer should be somewhere around 70.

Another helpful tip is to break down larger divisors into smaller factors. If you're dividing by 36, for example, you can divide by 4 and then by 9. This can simplify the process, especially if you're comfortable with dividing by smaller numbers. Just remember to keep track of your intermediate results.

Don't be afraid to use scratch paper! It's perfectly okay to write out your multiplication calculations on the side. Keeping things organized and clear will minimize the chance of making mistakes. Finally, and most importantly, practice, practice, practice! The more you do large division problems, the more comfortable and confident you'll become. Pretty soon, those intimidating numbers won't seem so daunting after all.

Frequently Asked Questions (FAQs)

6. Your Burning Questions Answered

Let's tackle some common questions about how to do large division.

Q: What if the divisor is larger than the first few digits of the dividend?

A: No problem! Simply look at more digits in the dividend until you have a number that the divisor can go into. For instance, if you're dividing 1234 by 56, 56 doesn't go into 12, so you look at 123 instead.

Q: How do I deal with zeros in the dividend or quotient?

A: Zeros can be tricky, but just remember to treat them like any other digit. If the divisor doesn't go into a portion of the dividend, write a '0' in the quotient and bring down the next digit. If you end up with a zero remainder and no more digits to bring down, you're done!

Q: Is there an easier way to do large division without long division?

A: Yes! While long division is a fundamental skill, calculators and computer programs are readily available to handle large division problems quickly and accurately. However, understanding long division is crucial for grasping the underlying concepts and developing a strong number sense. Plus, you never know when you might find yourself without a calculator, facing a division challenge in the wild!

Q: How much should I practice large division problems?

A: The amount of practice needed varies from person to person. However, start with a few problems a day and gradually increase the difficulty. Focus on understanding the process rather than just memorizing the steps. Once you feel comfortable, try tackling more complex problems with larger numbers and remainders. And most importantly, be patient with yourself and don't get discouraged if you make mistakes along the way. Everyone does! Really!